SCIENCE IN ANCIENT ARTWORK
By
Charles William Johnson
Within the maya long count numbers/fractals, the pictun number 2880000 appears to represent a strict relationship with similar fractals occurring in nature and in the general field of mathematics. It is understandable that many scholars shy away from the study of numbers, because one does not know what particular aspect obeys human design and which aspect obeys merely the manner in which numbers behave. In the Earth/matriX series, we have been attempting to distinguish these two aspects; numbers/fractals that occur in nature, and numbers/fractals that are historically significant (chosen by the ancients in their reckoning systems). Regarding the number/fractal 288, which lies on the maya long count series (36, 72, 144, 288, 576, 1152, 2304), we shall examine its relationship in some aspects of nature and mathematics. The case may be that the ancient maya chose the long count series of numbers/fractals because they reflect not only a constant series within mathematics, but also because they may be found in nature.
Initially, then, we find the 288 number/fractal within the maya long count series. We have also seen this particular number/fractal become instrumental in the arrangement of electrons in the elements of the periodic table (Cfr., Earth/matriX, Nos. 61 & 62). The extranuclear electron count for argon is 2•8•8, with a change of level occurring with the next element, potassium with the 2•8•8•1 arrangement. Let us observe a partial view of the periodic table, with some of the elements and their corresponding extranuclear electron count.
| 1 | 2 | 3 | 2 | 7 | 2 | 8 | 3 | 2 | 8 | 7 | 2 | 8 | 9 | 2 | 2 | 8 | 13 | 2 | 2 | 8 | 18 | 1 | etc | ||||||||||
| 2 | 2 | 4 | 2 | 8 | 2 | 8 | 4 | 2 | 8 | 8 | 2 | 8 | 10 | 2 | 2 | 8 | 14 | 2 | 2 | 8 | 18 | 2 | |||||||||||
| 2 | 1 | 2 | 5 | 2 | 8 | 1 | 2 | 8 | 5 | 2 | 8 | 8 | 1 | 2 | 8 | 11 | 2 | 2 | 8 | 15 | 2 | 2 | 8 | 18 | 3 | ||||||||
| 2 | 2 | 2 | 6 | 2 | 8 | 2 | 2 | 8 | 6 | 2 | 8 | 8 | 2 | 2 | 8 | 13 | 1 | 2 | 8 | 16 | 2 | 2 | 8 | 18 | 4 |
The element neon has a configuration of 2•8, which changes with sodium 2•8•1; then, argon 2•8•8, which changes with potassium 2•8•8•1. From the perspective of the logic of numbers, one would expect the 2•8•8•1 pattern to evolve through 2•8•8•8; but, change occurs scandium 2•8•9•2, whereby the third level of electrons jumps to 9. Nonetheless, the significant pattern involves the 2•8•8 beginning, and the fact that it is maintained throughout with changes at the third level. No matter what, one obtains the impression that 2•8•8 is the underlying pattern suggested from the outset of the extranuclear electron count of the elements. In other words, the pattern that is visibly suggested, and broken, is that of 2•8•8, for whatever reasons of the possibility/impossibility of electron stability at the third level.
Another example of the mathematical constant 288 exists within geometry and the relationships of equivaleny/inequivalency of the numbers of perfect right triangles. We have discussed this particular aspect in detail in previous essays (Cfr., Earth/matriX, Nos. 55, 56, 57 & 58). The regular, perfect right triangle series begins with the measurements 3•4•5. These measurements serve as the basis for the Pythagorean Theorem, whereby the square of the first two numbers, combined, equal the square of the third term. There exists another series of perfect right triangles, which may be determined as irregular, which begins with the measurement numbers 5•12•13, which also obeys the Pythagorean Theorem. Now, consider the difference between the numbers of the two distinct series of perfect right triangles:
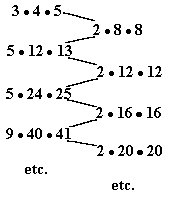
As one may observe from this series of numbers and differences, the 2•8•8 initial term begins the series with 2•8•8, with increments thereafter of 2•4•4. In 3 other words, two distinct series of perfect right triangles exist; one begins with the measurements 3•4•5 and the other with those of 5•12•13; and, the difference between these measurements is 2•8•8. As in the periodic table, we are observing now in geometry the reoccurrence of the terms 288 as an initial constant representing a change in level; a change from one series of of perfect right triangles to the other. In previous studies we have seen how the 3•4•5 and 5•12•13 numbers on a graph at right angles reflect the very design and layout of some of the pyramidal sites (Cfr., Earth/matriX, No.80).
Aside from these aspects of nature and mathematics, there might be a more direct observation of the significance of the 288 number/fractal within the maya long count system itself. In order to discern this point, we shall require examining the method of duplatio/mediatio and the maya companion number 1366560. From the previous example, it is relatively easy to see that in order to go from the first series of perfect right triangles (3•4•5) to the next series (5•12•13), must simply add 2•8•8 correspondingly to the numbers of the first. Regarding the maya companion number, 1366560, its significance is not so readily observed. In fact, today scholars do not appear to be in agreement as to exactly what the companion numbers mean (1366560 and 1385540). However, we have been analyzing them in relation to the maya long count and the ancient reckoning system of ancient kemi, and some computations appear to be relevant involving these particular numbers. Let us concentrate on the 1366560 companion number here.
Let us take two historically significant numbers, 25920 and 31104, and add them together for the sake of an example; then, we shall apply the doubling/halving method, and have the companion number enter the scene as well. Many examples may be chosen, but we shall offer only a couple, since once the reader observes the manner in which the numbers perform, it will be seen that this particular computation holds for any case. We have chosen more obvious historically significant numbers for this illustration.
|
Now, 458208 / 1591 = 288
Had we continued to divide 1591 by 3, the result would have been: 530.333; a fraction. It is often stated that the ancient maya avoided the fractions. In a sense, what we are observing is that their very system, the maya long count numbers/fractals, serve for computations with fractions. The companion number intervenes at one point in the computation whereby a number is achieved that results in a fractional relationship with the maya long count. Consider the following series based on doubling/halving the numbers:
|
Now, let us treble the original number:
|
In other words, the maya long count numbers/fractals, on this particular series of numbers as of the subtracting of the companion number, represent a constant number series, similar to that occupied by the more well-known constant series 1,2,4,8,16,32,64,128,256,512; a series which is used in modernday computers alongwith the maya long count constant series (Cfr., Earth/matriX Extract No.12). The last number evenly divisible by three on the series relates as of 288x to the first number appearing on the series after the companion number has been subtracted (since 601 / 3 = 200.333).
Let us present one more example with a previously cited number:
| 290304 | (= | 259200 + 31104) | ||
| 580608 | ||||
| 1161216 | - | 1366560 | = | 205344 |
| 205344 | (halved) | 6417 | / | 3 | = | 205344 | / | 713 = 288 | |||
| 102672 | 2139 | ||||||||||
| 51336 | 713 |
In other words, after subtracting the companion
number
|
|||||||||
| 25668 | 237.666 | 1366560, one obtains a number series (fractional or not) | |||||||||
| 12834 | in relation to the maya long count numbers/fractals | ||||||||||
Depending, then, upon the chosen direction, the number series in these cases begins/ends with the constant term 288; as one either goes into fractional expressions (for example, 237.666), or leaves fractional expressions (for example, 237.888). Prior to entering and leaving fractional computations, then, as of the maya companion number, one is always dealing with a number that relates 288 times with the product resulting from the maya companion number. In this manner, from the perspective of mathematical computations possible within the designed maya long count and the companion number, 1366560, one is faced with a mathematical constant of 288, which likewise begins or ends a series of numbers/fractals based on the maya long count (36, 72, 144, 288, 576, 1152, 2304) in relation to fractional/whole numbers.
From this perspective, the manner in which the maya long count is designed as of the companion number, we see a very similar procedure followed as to that witnessed within the change of levels within the extranuclear electron count of the elements as cited on the periodic table, and the translation between the two sets of perfect right triangles. In other words, the very design of the maya long count system, as we have examined it through possible computations as of its own terms (numbers/fractals), would appear to reflect the designs found in nature. One might want to conclude prematurely that all of these relationships are mere happenstance; coincidence. Yet, the fact that an historically significant number (1366560), which is obviously the result of humanly consious design and decision-making, i.e., by choice, would somehow keep us from simply attributing all of this coincidence to mere happenstance. In order to obtain the constant series, it would appear that human intervention had to be designed as of the companion number; that is, the companion number 1366560 was chosen with a specific computational purpose in mind. It results from a conscious design, and a specific kind of knowledge regarding the behaviour of numbers/fractals in the ancient reckoning system.
Reproduction prohibited without written consent of the author.
Your comments and suggestions are greatly appreciated:
e-mail: johnson@earthmatrix.com
Earth/matriX
Science in Ancient Artwork
Extract Nş.19
A Mathematical Constant: 288
July 15, 1997
©1997-2015 Copyrighted by Charles William Johnson. All Rights Reserved
Earth/matriX, P.O. Box 231126 New Orleans, LA 70183-1126;USA
| Home | Books | Forum | Reviews | Links | Author |