| Il linguaggio degli Dei |
|||||||||||||
Relazione tra la Camera del Re della Grande Piramide e il Tempio del Signore descritto nella Bibbia dal profeta Ezechiele A - Premesse Gli Antichi Patriarchi si esprimevano attraverso un alfabeto geometrico i cui elementi fondamentali erano: 1-punto
Nel lavoro che presentiamo dimostreremo che questo linguaggio geometrico è stato usato per creare un modello geometrico e definire le dimensioni della Camera del Re della Grande Piramide e del Sarcofago che si trova all'interno. B - Creazione del modello consideriamo un rettangolo di lati : a e b con b > a 
Poniamo per semplicità la larghezza a = 1 Calcoliamo l'elemento ( x ) tale che:
  e quindi x = 1 / b Calcoliamo ora la distanza tra i centri dei rettangoli simili così costruiti Tracciamo il cerchio di raggio d e centro , il centro del rettangolo (a;b)
Noto d è possibile costruire il triangolo rettangolo interno definito : "giallo" i cui cateti misurano: c2 = d/a*b/2
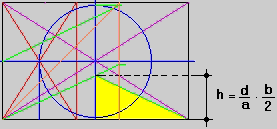
 Del modello geometrico così definito prendiamo in esame due casi particolari. Primo caso Esite un solo valore di b tale che d = a/2 =1/2
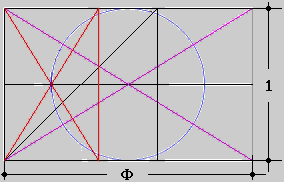
 Procediamo ad un ulteriore sviluppo geometrico considerando che e' sempre possibile procedere alla costruzione di una figura interna secondo la sequenza geometrica che segue:
  
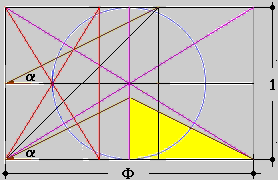
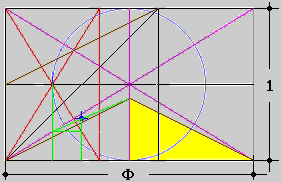
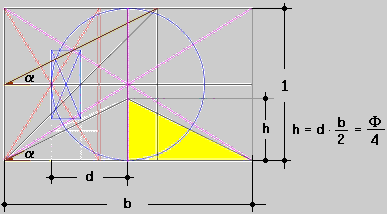
Si tratta di definire un rettangolo particolare interno alla figura
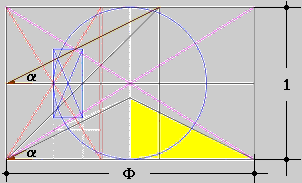
originaria. Secondo caso Se ora consideriamo il caso in cui b = 2 , descritto nel disegno seguente, scopriamo che questo, spiega perfettamente il perché dei rapporti presenti tra la Camera del Re e il Sarcofago della Grande Piramide.
 
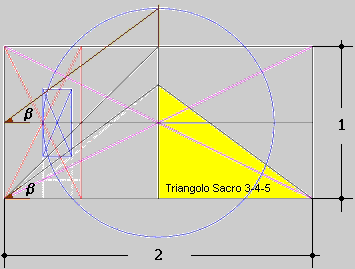
Confronto tra misure rilevate e modello geometrico le misure rilevate
espresse in cùbiti reali sono: lunghezza della Camera del Re - 20 CR - larghezza del Sarcofago - 1,878 CR - lunghezza del Sarcofago - 4,368 CR - altezza del Sarcofago - 2,001 CR (Si tratta di misure mediate perchè i manufatti presentano
lievi irregolarità. -lunghezza Sarcofago(Modello) - 4,375 CR La costruzione geometrica seguente spiega anche perché l'
altezza del Sarcofago (Modello) è pari a 2,000 CR.
Notiamo che è sempre la costruzione del triangolo rettangolo " giallo " che guida le sequenze geometriche che portano al dimensionamento del Sarcofago. Nel caso di b = 2 , il nostro triangolo è il Triangolo Sacro di Osiride 3-4-5 dove i tre lati rappresentano le divinità :
4- Iside 5- Horus ( vedi l'opera: "Iside e Osiride" di Plutarco) C - Confronto tra modello e Tempio del Signore descritto dal profeta Ezechiele Se ora procediamo alla sovrapposizione dei due modelli considerati primo caso : b = 1,618034... otterremo un modello complesso.
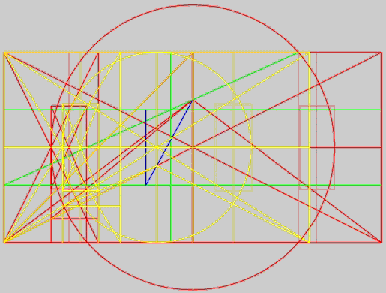
 Questo modello costituisce la struttura geometrica interna segreta
delTempio del Signore descritto da Ezechiele nella Bibbia ( capp.
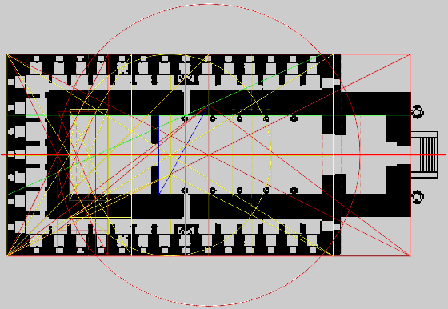
40 e seguenti) Ezechiele (Bibbia Cap.40...) Analisi Geometrica  D - Conclusioni Lo schema geometrico trovato deve essere considerato un modello di elevatissima risonanza armonica. La sua funzione potrebbe essere: permettere una percezione superiore della Realtà e un contatto con il Divino. Questo accade naturalmente se si riesce, per virtù personale, a trascendere la semplice osservazione razionale delle forme geometriche. Bibliografie: 1- La Bibbia : Ezechiele rubinoal@intercity.it All rights reserved | |||||||||||||
