Earth/matriX
Science Today
The Inverse Fine-Structure Constant,
The Ground State Energy Level of the Electron
in a Hydrogen Atom, and, The Earth/matriX
Thermodynamic Temperature Scale
[137.03599911 | -13.6eV | 1.3661]
By Charles William Johnson
Extract
| Possible relationships between some of the physical and chemical constants revolving within the 1.36 - 1.37 fractal range are treated in this essay. The ground state energy level of the electron in a Hydrogen atom shares a similar fractal value to the ratio of the boiling/freezing points of water on the thermodynamic temperature scale. The theoretical equation or formula of the inverse fine-structure constant presents an algebraic expression based on a redundancy of terms, which is critically analyzed and illustrated with a more economical expression. ----- summary. |
In previous essays, I have been pointing out the existence of a range of fractal values between 1.36 - 1.38 that occur in different aspects and constants of spacetime, matter-energy. In this essay, I examine the relationships of three distinct constants within that range. Other constants pertain to the solar constant (1.367), the Boltzmann Constant (1.3806505), for example, but will not be treated in this essay, although they have been reviewed in previous works. In these studies of the constants, the units of measurement or ratios are not being compared, but only the fractal numerical values themselves. Observations regarding the comparative analysis of units of measurement and ratios would require a much more extensive essay than the present one.
At one time, Sir Arthur Eddington proposed that the inverse fine-structure constant was 136. Physicists today measure it experimentally at 137.03599911 to be exact, and theoretically seek to derive it through an equation of selected terms as will be discussed below.
The ground state energy level of the electron in a Hydrogen atom is given generally as -13.6eV. In other words, it requires a -0.0000136 MeV to pull the electron from a Hydrogen atom. This is also known as the binding energy, since it requires that same amount of energy, it is reasoned, to hold the Hydrogen atom together. In a sense, then, the -13.6 eV energy is the binding/unbinding energy of the Hydrogen atom.
The ratio between the boiling point of water and the freezing point of water on Earth is 1.366099213 as: 373.15 Kelvin divided by 273.15 Kelvin yields 1.366099213. The 1.366099213 fractal value may be rounded off to 1.3661 for all practical purposes. Given the fact that energy is added to frozen water in order to convert it to boiling water, it is not surprising to observe a coincidence in numerical values with the ionization energy of Hydrogen. Water consists of Hydrogen and Oxygen (H20). Hence, one would expect the numbers relating to the ionization of Hydrogen to be relational to the boiling/freezing points of water (Hydrogen and Oxygen).
Thus, I find it logical to find a similar fractal value for the binding/unbinding energy of Hydrogen (1.36 fractal), and the thermodynamic temperature scale as of the ratio 1.3661 relating to the boiling/freezing points of water (Hydrogen2 plus Oxygen). It is generally stated that the principal reason that water stays together is precisely due to the Hydrogen bond between the oxygen and hydrogen atoms. Further, the hydrogen bonds in water are the main reason for the high freezing (or, melting) and boiling points of water.
Take note then of the following values. The radius of 1-Hydrogen is 1.2 Å and that of 6-Oxygen is 1.4 Å. The length of the covalent bond between Oxygen and Hydrogen is 0.95 angstroms. Consider then:
| 1.2 / 0.95 |
=
|
1.263157895 |
| 1.4 / 0.95 |
=
|
1.473684211 |
| 1.263157895 plus 1.473684211 equals 2.736842106 |
| 2.736842106 / 2 = 1.368421053 mean |
Another option in the computation: 1.2 + 1.4 = 2.6 / 2 = 1.3 / 0.95 = 1.368421053.
Note the reciprocal of this value: 1 / 1.368421053 = .73076923 (halves to .365384615). Note the sidereal count of Earth's orbital time in fractal expression: 1 / .365256 = 2.737805813 (halves to 1.368902906). Boiling water at 100 degrees Celsius needs 540 cal/g as heat of vaporization (multiples thereof 540, 270, 135...).
Here is one datum that I found recently. In an article entitled, "Water and Ice", by Alan K. Super in the magazine Science, August 23, 2002, he states: "The glass transition temperature for water is in fact much lower, probably around 136K". Consider also, the Schaefer Point refers to the common value on the Centigrade and Fahrenheit scales: 40 °C = -40 °F. A similar point of coincident values appears on the Centigrade and Kelvin scales: -136.575 °C = 136.575 K.
Sir Arthur Eddington, with an indecipherable reasoning behind his computations, proposed the use of a value of 136 for the reciprocal of the inverse fine-structure constant (102 + 62 = 136). He reluctantly succumbed to pressure from his peers and adopted the theoretical 137 fractal number. This value today is computed experimentally to be 137.03599911. After examining the fractal values, the case may be that Eddington simply employed intuition to derive a number that may be relational to the inverse fine-structure constant.
Over time, various theoretical exercises have been pursued to establish the exactness of the 137c fractal value. Selected examples, supposedly based in physics and which are commonly cited in the literature concern the following examples: [The following values are cited in the book, The Constants of Nature by John D. Barrow, Pantheon, New York, 2003, 368 pages. A great read; highly recommended.]
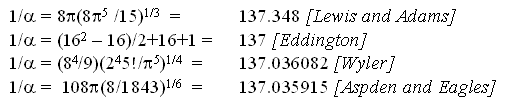
Other playful 137 numerology exercises are:
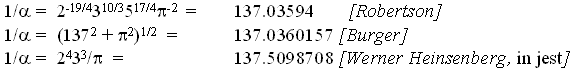
In my studies of ancient reckoning numbers, I have toyed with the concept of fractional powers to whole numbers, as used in some of the previous examples shown here. Yet, in reality, as a spacetime event, as an event of matter-energy, it is impossible to multiply, say, 3 times itself 10/3 times or, 3 to the 3.33333333 power. The exponent is a shorthand algebraic notation. Of course, such a fractional expression can be carried out on electronic calculators as those being produced today. But, in reality, there is no spacetime event, no physical event of matter that would allow itself to undergo such a procedure. Even the numbers themselves, such as the number 3 in this example, will not allow themselves to function as such: 3 times itself 3.33333333 times.
I can only marvel at how the electronic calculators are programmed to achieve 8191.36656 equals 9575.84811. The only term that may exist of the previous three expressions is that of 819 (as an 819 quantity of something), whereas the power 1.36656 and the product, 9575.84811 reflect pure magic in numbers. To put it succinctly: people will never hold in their hands 21.36656 of something, nor multiply the number by itself 1.36656 times ---other than as effected on the small pocket calculators of today.
And, so it goes with the previously cited examples regarding
the 137c number. One may express algebraically a fractional exponent as
in one of the previous examples, say, 1/![]() = 8
= 8![]() (8
(8![]() 5 /15)1/3 = 137.348 [Lewis
and Adams]. [In fact, on my calculator this equation derives 1367.309075.]
5 /15)1/3 = 137.348 [Lewis
and Adams]. [In fact, on my calculator this equation derives 1367.309075.]
But in terms of spacetime events, say, the term 157/4 ---to use any term as an example of fractional exponents---, does not reflect a spacetime (matter-energy) event. The number 15 may be multiplied in practicality by itself any whole number of times; in theoretical abstraction, however, 15 may be multiplied by itself any fractional number of times. However, the numbers obtained from the former may reflect the existence of the resulting number of matter-energy events; the latter are numbers resulting from the theoretical computations but do not represent or reflect actual spacetime, matter-energy events. 15 apples times 15 apples means 225 apples. While, according to my pocket electronic calculator the following obtains, given 17 / 4 = 4.25:
|
154.25 = 99629.47711
|
Either way, the numbers mean nothing because there are no fractional apples whose multiplication together would yield such a number, nor a fractional exponent that would yield such a fractional number in terms of spacetime events at least. Fractional exponents are a question of algebraic notation; they do not concern the behavior of matter-energy events.
You may find a combination of numbers and powers that produce even the 1.370359991-number (as illustrated in this essay), but that does not mean necessarily that that algebraic expression expresses anything. For example, the square of the elementary particle divided by the reduced Planck constant times the reciprocal of the speed of light in a vacuum equals 137.0359991, may be derived. But the question remains whether this equation reflects the actual events under consideration. Think about it, the reciprocal of the speed of light in a vacuum does not exist, just as the square of the speed of light in a vacuum does not exist in matter-energy. The speed of light in a vacuum is such a value as said to be a fixed limit to the speed of any matter-energy event in spacetime. Hence, the square of that limit is a purely theoretical construct, not a practical event.
Nonetheless, within the list of physical and chemical constants, one finds the Hertz-Inverse Meter Relationship to be expressed as fractal "3.335640951 e-9 (exact) m-1". Again, this is a fractal value of the reciprocity of the speed of light in a vacuum: 1 / 3.335640951 = .299792458. And, given the exactness with which the constant for the speed of light in a vacuum is presented, so it goes with the particular constant cited here.
Physicists look down upon the numerical meanderings of numerology in the study of matter-energy. Yet, as may be seen from the inverse fine-structure constant below, it would appear as though the physicists themselves are not far from falling into numerology, numbers for the sake of numbers.
To date, the various and changing expressions of the fine-structure constant and its inverse expression cause doubt as to whether at some future point in time, physicists may ultimately adjust the 137.03599911 number in use today for a distinct value; maybe even one closer to Sir Arthur Eddington's number (136c). However, for some time now the search has been on to find the most precise fractional expression of the inverse fine-structure constant. Physicists shy away from an expression of 137.036 for the supposed more exact measurement of 137.0599911 (through possibly 137.0599946).
The point then to be made, in my mind, is as follows. The previously cited value of -13.6 eV for the ionization of neutral Hydrogen reflects a specific spacetime/movement event in matter-energy. The 1.3661 ratio of the boiling/freezing points of water reflects a specific ratio or proportion of spacetime/movement events in matter-energy. While, the fine-structure constant and its inverse expression supposedly reflect a specific spacetime/movement event in matter-energy, the distance between an electron and a photon under certain circumstances. Yet, the algebraic formula that states the manner in which the 137.03599911 value is derived, in my view, confounds more than clarifies. And, I do not feel that this is a self-inflicted confusion, but rather one that derives from the redundancy of the terms cited in the equation. Let me illustrate the point.
The inverse fine-structure constant is symbolized as follows:

This equation would read as, the square of the elementary particle is divided by the reduced Planck constant times the speed of light in a vacuum times four pi times the permittivity of free space. Let me place the corresponding values to each of the cited terms as follows:
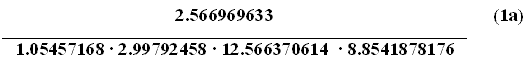
The result from the previously cited equation, then, is fractal 7.297352573, close to the value generally given today for the fine-structure constant (7.297352568) ---[my pocket calculator has its limits].
Now, the previous formula as stated is but a shorthand version
for the notation of some of its terms. In other words, the reduced Planck
constant h bar, ![]() ,
actually represents the Planck constant times
two pi, h/2pi, and the permittivity of free
space
,
actually represents the Planck constant times
two pi, h/2pi, and the permittivity of free
space ![]() actually represents the reciprocal of the speed of light in a vacuum squared
times the permeability of vacuum, 1/c2
actually represents the reciprocal of the speed of light in a vacuum squared
times the permeability of vacuum, 1/c2![]() . The expression
. The expression ![]() is the electric constant (8.8541878176),
and the expression
is the electric constant (8.8541878176),
and the expression ![]() is the magnetic constant, which
itself is four pi (12.566370614).
is the magnetic constant, which
itself is four pi (12.566370614).
Consider the longhand expression then of the previous equation with its symbolic notation filled in, i.e., without any abbreviation or substitution of its terms:
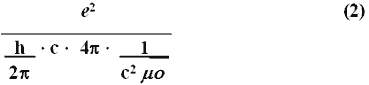
The unabbreviated expression would then read as follows: the square of the elementary particle (e2) is divided by the reduced Planck constant, which represents the Planck constant, in turn divided by two pi times the speed of light times four pi times the permittivity of free space which itself represents, one divided by the speed of light in a vacuum squared times the permeability of vacuum.
Much of the discourse in mathematics and physics remains at the level of providing insight into the algebraic expressions and their notation, without ever actually presenting the numbers represented by the equations themselves. So, once again, let us fill in the numerical values relating to the constants cited in the equation in order to observe how they perform. Therefore, translate the previous algebraic notation into their fractal numerical expressions and the following obtains:
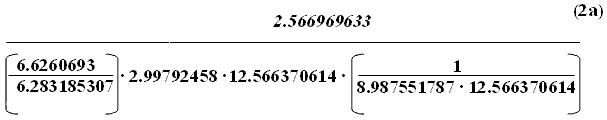
One cannot help but notice the redundancy of the terms for pi and for the speed of light in a vacuum (12.566370614; given 2.99792458 times 2.99792458 = 8.987551787). And, if you tell me that they cancel out one another, then, the logical response is to question why have them in the equation in the first place, since they serve no computational purpose. Any term cancelled out in an expression is as though it did not exist, meaning that the notational expression requires rewriting in order to uncover the base relationship within the equation. Further, the initial equation (1) is not a more synthetic expression of the latter formula cited above (2), since even though the former contains fewer terms, its terms are based upon and, necessarily include, the expanded terms of the second equation.
The redundant terms of this equation (c and pi) are hidden in the algebraic notation shown in the previous formula for the inverse fine-structure constant (1) as becomes evident in the following indication.
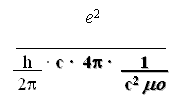
The terms c • 4pi times
1/c2![]() represent in fact c • 4pi times
1/c2 4pi. And, with that, the
divisor of the formula given for the inverse of the fine-structure constant,
states similar terms twice in a distinct but obviously redundant fashion.
The distinction that c • 4pi
differs from 1/c2 4pi because
of the reciprocity and squaring of c in the latter expression is irrelevant
in nature, once the actual computation of the terms is carried through
to their numerical values as will be shown below.
represent in fact c • 4pi times
1/c2 4pi. And, with that, the
divisor of the formula given for the inverse of the fine-structure constant,
states similar terms twice in a distinct but obviously redundant fashion.
The distinction that c • 4pi
differs from 1/c2 4pi because
of the reciprocity and squaring of c in the latter expression is irrelevant
in nature, once the actual computation of the terms is carried through
to their numerical values as will be shown below.
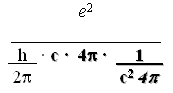
Consider then,
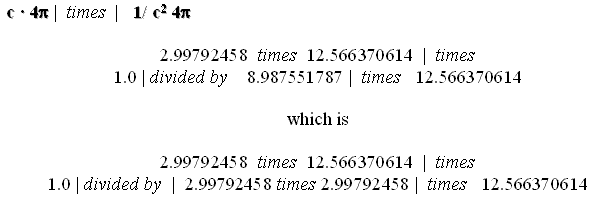
In this manner, one may observe how the four apparently
distinct terms actually produce the reciprocal
of the speed of light in a vacuum, since
| c • 4pi | times | 1/ c2 4pi equals fractal .333564095 |
| 1 / .333564095 equals 2.99792458 fractal speed of light in vacuum |

Now, consider, the fractal numerical expression of these
terms as follows:
2.566969633 (e2) divided
by 1.05457168 (h/2pi) times
.333564095 (1/c) yields
1.05457168 times .333564095 x = .351767248
and,
2.566969633 / .351767248 = .13703599911 inverse
fine-structure constant
And, if one prefers the use of the reduced Planck Constant, then, for the fine-structure constant, 7.29735257, as shown in some computations for electrostatics of today, one has the fine-structure constant as:

In my mind, given the usage of the previous equation (3), the expression for the inverse fine-structure constant, 1.3703599911, as shown here without the apparent redundancies better portrays the theoretical reciprocity of the fine-structure constant. In summary, canceling out the redundant terms, the algebraic expression of the inverse fine-structure constant would be:

In this case, the reciprocal of the speed of light in a
vacuum is employed as the complementary term in the divisor together with
the reduced Planck constant. In the expression (3), the term 4![]()
![]() is taken as dimensionless constant 1. However, in summary, the expression
c • 4pi times 1/c2
is taken as dimensionless constant 1. However, in summary, the expression
c • 4pi times 1/c2![]() represents in fact c • 4pi times
1/c2 4pi, the reciprocity of the speed of
light in a vacuum. Within the divisor of the expression formula given
for the inverse of the fine-structure constant (2), one has redundantly
stated similar terms only in a modified form:
represents in fact c • 4pi times
1/c2 4pi, the reciprocity of the speed of
light in a vacuum. Within the divisor of the expression formula given
for the inverse of the fine-structure constant (2), one has redundantly
stated similar terms only in a modified form:
c • 4pi | times | 1/ c2 4pi
The cancellation of redundant terms yields 1/c. The reduced expression for the inverse fine-structure constant (4) obtains once the redundancy of terms is cancelled in the algebraic notation of the equation.
As a material event, one may visualize the spacetime event represented in the -13.6 eV energy level required for pulling an electron from a Hydrogen atom. As another material event, it is also possible to visualize the 1.3661 value for the proportion of the boiling/freezing point of water. But, it remains beyond my comprehension how to visualize the algebraic expression of the fine-structure constant (7.297352568) and its inverse constant (137.03599911) as expressed in the formulae generally cited in the literature of physics as given above in equations (1) and (2).
There is little problem in comprehending the distance between an electron and a photon, so to speak; the question arises regarding the algebraic notation employed to express that material event. It seems beyond reason and logic to create a formula or equation that contains redundant terms, whose cancellation itself serves no purpose. In other words, instead of stating c • 4pi | times | 1/ c2 4pi, the purpose of comprehension may be better served by stating simply 1/c, since this is what is actually being affirmed by that cluttered expression.
It appears more relevant to comprehend the inverse fine-structure, as of the reciprocal of the speed of light in vacuum, then as of its supposed relationship (squared) to that of 4pi. Again, pi exists as of the relationship of a circle to its diameter. The concept of four pi is merely conceptual, given the fact that four pi could in fact pertain to four circles, each with its expression of pi, and so on.
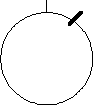 |
Pi relational to the distance on a circle; i.e., 3.141592654 diameters marked off on the circumference of a circle. In order to mark off four pi, one would have to trace over the distance on the circumference or, draw out four different circles with pi marked on each one. In other words, four pi as such does not exist other than as a theoretical concept in the computations. |
The foregoing cannot be reduced to a mere discourse of numbers (i.e., studies in numerology). To employ redundant expressions in the equations suggests a certain degree of numerology, given the fact that terms/numbers appear in the equation that reflect no visible spacetime coordinate. So, the question always remains whether the fractals/numbers reflect in fact spacetime/motion events that exist in matter-energy. Given that the fine-structure constant is not a mere statement of belief, but one of cognitive experimental measurement, one would expect its theoretical expression to exactly reflect relationships (of multiplication and division) that exist in reality, i.e., in spacetime/motion, in matter-energy.
The precision sought in theoretically rendering the numerical value of the inverse fine-structure constant as 137.0599911(46) becomes suspect, in my view, when one considers that the exactness being sought in its measurement is based upon redundant theoretical computations as illustrated in this essay. A goal of economy in the computations was foremost with the invention of algebraic notation in mathematics. However, I often find that some of the computations effected in algebraic notation today present excess and redundancy, and not an economy of terms.
Table of Matter-Energy Events and Corresponding Fractal Values
| Ionization Energy of Hydrogen |
The ionization energy of hydrogen is:
|
-13.6 eV. |
| Solar Constant |
The solar constant is:
|
1.367 w/m2. |
| Thermodynamic Temperature Scale |
The thermodynamic temperature reflects the 1.3661
ratio between the boiling and freezing points of water.
|
1.3661 |
| The Inverse Fine-Structure Constant |
The Fine-Structure Constant and the Inverse Fine-Structure
Constant are 7.297352568 and 137.03599911 respectively
|
137.03599911 |
| Hartree Energy |
Hartree energy
27.2113961 / 2 = 13.60569805 |
13.60569805 |
| Rydberg Constant |
Rydberg constant 13.6056981[same as Hartree energy
half value]
|
13.6056981 |
| Core-Mantle Boundary |
136 Gigapascals of pressure at the Core-mantle
boundary
|
136 Gigapascals |
| Newtonian Constant of Gravitation |
The Newtonian Constant of Gravitation:
|
6.6742 is a multiple of 13668.7616 |
| Sidereal Year of Earth |
The Sidereal Day-Count of Earth:
|
365.256 is a reciprocal multiple of .0013689254 |
| Velocity of Light |
The Speed of Light is a reciprocal of:
|
1.366278534 |
| Refractive Index of Light |
The Refractive Index of Light:
|
1.3669 |
| Electron to Alpha Particle Mass Ratio |
The Electron to Alpha Particle Mass Ratio is given
as a constant value:
|
1.370933555 |
| The Boltzmann Constant |
The Boltzmann Constant and/or the Kelvin-Joule
Relationship is:
|
1.3806505 |
|
"Living cells typically have a refractive index
of between 1.33 and 1.38." Approximately 1.36 is the average of
these two cited values.
|
1.36 |
The Reciprocal of 136 Fractal
Further consider the reciprocal multiples of the 136c fractal value.
| 1 / .136 | = | .7352841176 |
| .367647058 | ||
| .183823529 |
The reciprocal of 136 fractal, then, halves down to 1.83823529 fractal, which is suggestive of the neutron-electron mass ratio: 1838.6836598.
Consider the fractal expression of the neutron-electron mass ratio, which is very near the 1.36 fractal mark:
| 1 / .18386836598 | = | 5.43867345 |
| 2.719336725 | ||
| 1.359668363 |
Earth/matiX
SCIENCE TODAY
River Ridge, Louisiana 18 November 2006
©2006-2010 Copyrighted by Charles William Johnson. All rights reserved.
Earth/matriX: Science in Ancient Artwork. ISBN 1-58616-451-1
Earth/matriX Editions
email:johnson@earthmatrix.com
| Home | Books | Forum | Reviews | All Essays | Author |